Question

14. A satellite orbits 22, 300 miles above the equator. It completes one revolution in 24 hours. Assume that the radius of the Earth is 3, 960 miles. How far will the satellite travel in one day?​

Answer 1

Displacement = 0 mi

Distance = 164,996.45 mi

Explanation:

In this case, the displacement will be zero because the satellite goes back to its starting point after one day. If there is no distance traveled between the starting point and the ending point, then the Displacement will be zero.

When it comes to the distance, we will need to calculate the perimeter of the circle the satellite describes when making one whole turn around the earth.

The perimeter of a circle is given by the equation:

`p=2\pi r`

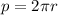
so we need to start by finding what the radius of the circle is. This radius if found by adding the radius of the earth and the distance above the equation the satellite is located at, so we get that:

`r=r_(earth)+h`

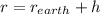
where h is the height of the satellite, so the radius of the circle is:

`r=22,300mi + 3,960 mi`

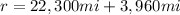
so

r=26,260 mi

so now we can use the perimeter equation to get:

`p=2\pi r`

`p=2\pi (26,260)`

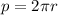
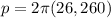
So the distance traveled by the satellite in one day will be:

P=164,996.45 mi.