Question

A medical researcher needs 37 people to test the effectiveness of an experimental drug. If 101 people have volunteered for the test in how many ways can 37 people be selected

Answer 1

The number of ways to select 37 people from 101 is, 5,397,234,129,638,871,133,346,507,775.

Explanation:

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!\cdot (n-k)!)`

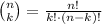
Compute the number of ways to select 37 people from 101 as follows:

`{101\choose 37}=(101!)/(37!\cdot (101-37)!)`

`=(101!)/(37!* 64!)\\\\=(101* 100* 99*....64!)/(37!* 64!)\\\\=5397234129638871133346507775`

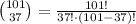
Thus, the number of ways to select 37 people from 101 is, 5,397,234,129,638,871,133,346,507,775.