Question

1.) We can write a equation of a line when we know only the slope and the _____________ of any point of the line.

2.) Given only two points, it is easy to find the equation of the line when you find first the _______________.

Answer 1

1) coordinates

2) slope

Explanation:

The equation of a line is given by the two equations:

`y=mx+b`, where m is the slope and b is the y-intercept, or

`y-y_1=m(x-x_1)`, where x₁ and y₁ is the location of any point on the line, and m is the slope.

→ As such, we know that given the slope and the coordinates of any point on a line, we can write the line's equation.

We can also find the slope of a straight line between two points with the following equation:

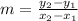`m = (y_2-y_1)/(x_2-x_1)`, where m is the slope, x1 and y1 is the location of the first point, and x2 and y2 is the location of the second point. Remember: rise (y) over run (x).

→ So, given only two points, it is easy to find the equation of the line when you first find the slope.