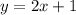Question

Find an equation of the tangent to the curve f(x) = 2x2 - 2x + 1 that has slope 2

Answer 1

D. y = 2x + 1

Explanation:

The tangent to the curve has one point in common with the curve.

The slope-intercept form of an equation of a line:

`y=mx+b`

`m` - slope

`b` - y-intercept

We have the slope
`m=2`.

`y=2x+b`

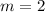Therefore we have the system of equations:

`\left\{\begin{array}{ccc}y=2x^2-2x+1&(1)\\y=2x+b&(2)\end{array}\right`

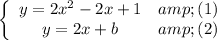
substitute (1) to (2):

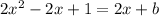`2x^2-2x+1=2x+b` subtract 2x from both sides

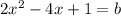`2x^2-4x+1=b` subtract b from both sides

`2x^2-4x+1-b=0`

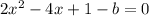
Use the discriminant of a quadratic equation:

`ax^2+bx+c=0\to \Delta=b^2-4ac`

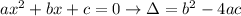
If Δ = 0, then we have one common point.

Calculate:

`2x^2-4x+1-b=0\\\\\Delta=(-4)^2-4\cdot2\cdot(1-b)=16-8+8b=8-8b`

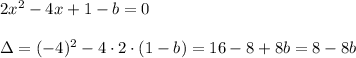
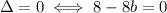`\Delta=0\iff8-8b=0` subtract 8 from both sides

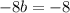`-8b=-8` divide both sides by (-8)

`b=1`

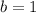
Finally:

`y=2x+1`