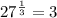Question

What is the simplified value of the exponential expression 27}?

оооо
3
9
1/3
1/9

Answer 1

Note: Your exponential expression seems a little unclear. Because 27 is not an exponential expression.

But, I am assuming that your exponential expression is:

• 
  `\:27^{(1)/(3)}`

The reason is that my solution would still clear your concept about this topic, no matter what the question is.

Answer:

The simplified value of the exponential expression is:

`27^{(1)/(3)}=3`

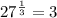
Explanation:

Assuming the exponential expression

`\:27^{(1)/(3)}`

`\mathrm{Factor\:the\:number:\:}\:27=3^3`

`=\left(3^3\right)^{(1)/(3)}`

`\mathrm{Apply\:exponent\:rule}:\quad \left(a^b\right)^c=a^(bc),\:\quad \:a\ge 0`

`\left(3^3\right)^{(1)/(3)}=3^{3\cdot (1)/(3)}`

`=3^{3\cdot (1)/(3)}`

`=3^1`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^1=a`

`=3`

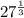
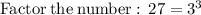
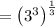
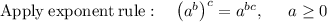
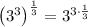
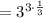
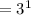
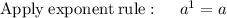
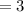
Therefore, the simplified value of the exponential expression is:

`27^{(1)/(3)}=3`