Question

A plane is flying due west at 34 m/s. It encounters a wind blowing at 19 m/s south. Find the resultant veloci

Answer 1

The resultant velocity has a magnitude of 38.95 m/s

Step-by-step explanation:

Vector Addition

Given two vectors defined as:

`\vec v_1=(x_1,y_1)`

`\vec v_2=(x_2,y_2)`

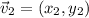
The sum of the vectors is:

`\vec v=(x_1+x_2,y_1+y_2)`

The magnitude of a vector can be calculated by

`d=√(x^2+y^2)`

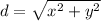
Where x and y are the rectangular components of the vector.

We have a plane flying due west at 34 m/s. Its velocity vector is:

`\vec v_1=(-34,0)`

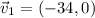
The wind blows at 19 m/s south, thus:

`\vec v_2=(0,-19)`

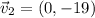
The sum of both velocities gives the resultant velocity:

`\vec v =(-34,-19)`

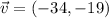
The magnitude of this velocity is:

`d=√((-34)^2+(-19)^2)`

`d=√(1156+361)=√(1517)`

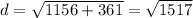
d = 38.95 m/s

The resultant velocity has a magnitude of 38.95 m/s