Answer:
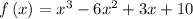 is the function of the least degree has the real coefficients and the leading coefficients of 1 and with the zeros -1, 5, and 2.
is the function of the least degree has the real coefficients and the leading coefficients of 1 and with the zeros -1, 5, and 2.
Explanation:
Given the function
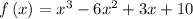
As the highest power of the x-variable is 3 with the leading coefficients of 1.
- So, it is clear that the polynomial function of the least degree has the real coefficients and the leading coefficients of 1.
solving to get the zeros
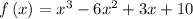
 ∵
∵
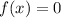
as

so
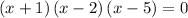
Using the zero factor principle
if
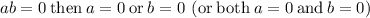
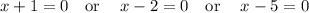
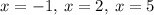
Therefore, the zeros of the function are:
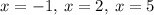
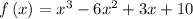 is the function of the least degree has the real coefficients and the leading coefficients of 1 and with the zeros -1, 5, and 2.
is the function of the least degree has the real coefficients and the leading coefficients of 1 and with the zeros -1, 5, and 2.
Therefore, the last option is true.