Question

Determine the remaining sides and angles of the triangle ABC

what is the measure of angle B

what is the length of side a

what is the length of side b​

Answer 1

The measure of angle B is 41.5°

The length of side a is 30.6 feet ⇒ to the nearest tenth

The length of side b is 32.9 feet ⇒ to the nearest tenth

Explanation:

• The sum of the measures of the interior angles in a triangle is 180°

In the given Δ ABC

∵ m∠A = 38.1°

∵ m∠C = 100.4°

→ By using the fact above

∵ m∠A + m∠B + m∠C = 180°

∴ 38.1 + m∠B + 100.4 = 180

→ Add the like terms in the left side

∴ 138.5 + m∠B = 180

→ Subtract 138.5 from both sides

∴ m∠B = 41.5°

∴ The measure of angle B is 41.5°

∵ a is the opposite side of ∠A

∵ b is the opposite side of ∠B

∵ c is the opposite side of ∠C

→ By using the sine rule

∴
`(a)/(sinA)` =
`(b)/(sinB)` =
`(c)/(sinC)`

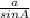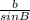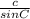
∵ c = 48.4 ft, m∠A = 38.1°, m∠B = 41.5°, and m∠C = 100.4

→ Substitute them in the sine rule above

∴
`(a)/(sin38.1)` =
`(b)/(sin41.5)` =
`(48.4)/(sin100.4)`

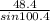
→ By using cross multiplication between the 1st and the 3rd fractions

∴ a × sin 100.4 = 48.8 × sin 38.1

→ Divide both sides by sin 100.4

∴ a = 30.61429861

∴ The length of side a is 30.6 feet ⇒ to the nearest tenth

→ By using cross multiplication between the 2nd and the 3rd fractions

∴ b × sin 100.4 = 48.8 × sin 41.5

→ Divide both sides by sin 100.4

∴ b = 32.87596206

∴ The length of side b is 32.9 feet ⇒ to the nearest tenth