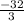Question

Find the volume of the tetrahedron with the given vertices. (2, 0, 0), (0, 4, 0), (0, 0, 4), (2, 4, 4)

Answer 1

The volume of the tetrahedron is

`(-32)/(3)`

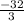
Explanation:

To find the volume of a tetrahedron with vertices (2, 0, 0), (0, 4, 0), (0, 0, 4), (2, 4, 4).

We know by definition that the volume of a tetrahedron with vertices
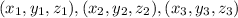`(x_(1), y_(1), z_(1)), (x_(2), y_(2), z_(2)), (x_(3), y_(3), z_(3))` is

`(1)/(6)\begin{vmatrix}</p><p>2 & 0 & 0 & 1\\</p><p>0 & 4 & 0 & 1\\</p><p>0 & 0 & 4 & 1\\</p><p>2 & 4 & 4 & 1</p><p>\end{vmatrix}`

From here we have:

`(1)/(6)\begin{vmatrix}</p><p>x_1 & y_1 & z_1 & 1\\</p><p>x_2 & y_2 & y_2 & 1\\</p><p>x_3 & y_3 & z_3 & 1\\</p><p>x_4 & y_4 & y_4 & 1</p><p>\end{vmatrix}`

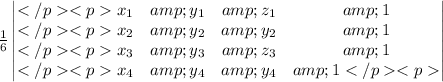
Finding the determinant of that matrix we have:

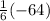`(1)/(6) (-64)` =
`(-32)/(3)`