Question

In the square pyramid shown below, the diagonal length FC = 16√2 centimeters and the height of the pyramid is 7 centimeters. Find the slant height AD of the pyramid, to the nearest tenth. Show your work with reasoning for each step.

Answer 1

Don't have

Explanation:

In the square pyramid shown below, the diagonal length FC = 16√2 centimeters and the height of thid, to the nearest tenth. Show your work with reasoning for each step. stepstep

Answer 2

The slant height AD of the pyramid is approximately 13.06 centimeters.

To find AC, we can use the Pythagorean Theorem in Triangle AFC:

`AC^2 = (16√(2) )^2 - 7^2`

`AC^2 = 256 * 2 - 49`

`AC^2 = 491`

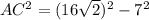
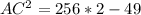
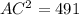
AC = √491 = 22.1 cm (since AC is half the diagonal length)

Since AC is the diameter of the base square, its midpoint is half the length of AC. Therefore, FD = AC/2 = 22.1 cm / 2 = 11.05 cm (nearest tenth)

Finally, we can use the Pythagorean Theorem in Triangle ADF to find AD:

`AD^2 = 7^2 + 11.05^2`

`AD^2 = 49 + 121.6025`

`AD^2 = 170.6025`

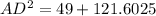
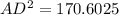
AD = 13.06 cm