Answer:
For the function:
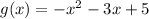 , the average rate of change of function over the interval
, the average rate of change of function over the interval
 is 2
is 2
Explanation:
We are given function:
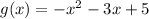 , we need to find average rate of change of function over the interval
, we need to find average rate of change of function over the interval

The formula used is:
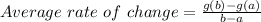
We have b=2 and a= -7
Finding f(b) and f(a)
Finding g(b) by putting x=2
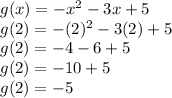
Finding g(a) by putting x=-7

Now, finding average rate of change when g(b)=-5 and g(a)=-23
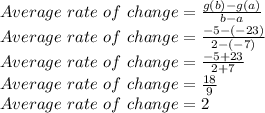
So, Average rate of change = 2
Therefore for the function:
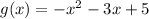 , the average rate of change of function over the interval
, the average rate of change of function over the interval
 is 2
is 2