Question

A man wants to cut down a tree in his yard. To ensure that the tree doesn’t hit anything he needs to know the height of the tree. He measures his distance from the tree at 18 meters and the angle of elevation to the tree at 80 degrees. What is the height of the tree to the nearest tenth of a meter?

Answer 1

`\boxed {\boxed {\sf 102.1 \ meters}}`

Explanation:

Let's assume the tree forms a right angle with the ground.

The distance from the tree to the man is 18 meters. The angle of elevation, which is 80 degrees, is the angle from where the man is to the top of the tree. We want to find the height of the tree, which we can call x.

Let's draw a diagram. (not to scale)

We can use sine (opposite/hypotenuse), cosine (adjacent/hypotenuse) or tangent (opposite/adjacent). We base the sides off of the elevation angle.

x is opposite the elevation angle and 18 is adjacent to the angle. So, we must use tangent.

`tan(\theta)=opposite/adjacent`

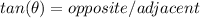
The angle (θ) is 80. The opposite is x. The adjacent is 18.

`tan(80)=x/18`

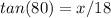
Now, solve for x by isolating it.

x is being divided by 18. The inverse of division is multiplication. Multiply both sides of the equation by 18.

`18*tan(80)=x/18*18`

`18*tan(80)=x`

`18*5.67128182=x`

`102.0830728=x`

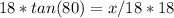
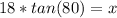
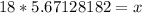
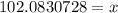
Round to the nearest tenth. The 8 in the hundredth place tells us to round up.

`102.1\approx x`

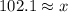
The height of the tree is about 102.1 meters.

**diagram is not to scale