Answer:
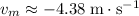 (moving toward the incline.)
(moving toward the incline.)
 (moving away from the incline.)
(moving away from the incline.)
(Assumption:
 .)
.)
Step-by-step explanation:
If
 , the potential energy of the block of
, the potential energy of the block of
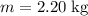 would be
would be
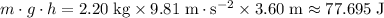 when it was at the top of the incline.
when it was at the top of the incline.
If friction is negligible, all these energies would be converted to kinetic energy when this block reaches the bottom of the incline. There shouldn't be any energy loss along the horizontal surface, either. Therefore, the kinetic energy of this
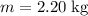 block right before the collision would also be approximately
block right before the collision would also be approximately
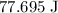 .
.
Calculate the velocity of that
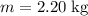 based on its kinetic energy:
based on its kinetic energy:
 .
.
A collision is considered as an elastic collision if both momentum and kinetic energy are conserved.
Initial momentum of the two blocks:
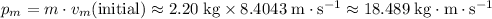 .
.
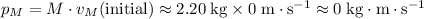 .
.
Sum of the momentum of each block right before the collision: approximately
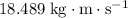 .
.
Sum of the momentum of each block right after the collision:
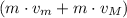 .
.
For momentum to conserve in this collision,
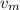 and
and
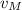 should ensure that
should ensure that
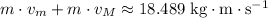 .
.
Kinetic energy of the two blocks right before the collision: approximately
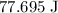 and
and
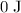 . Sum of these two values: approximately
. Sum of these two values: approximately
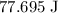 .
.
Sum of the energy of each block right after the collision:
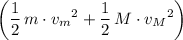 .
.
Similarly, for kinetic energy to conserve in this collision,
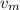 and
and
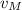 should ensure that
should ensure that
 .
.
Combine to obtain two equations about
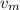 and
and
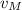 (given that
(given that
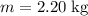 whereas
whereas
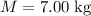 .)
.)
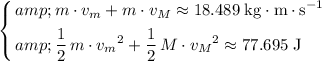 .
.
Solve for
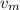 and
and
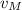 (ignore the root where
(ignore the root where
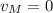 .)
.)
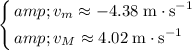 .
.
The collision flipped the sign of the velocity of the
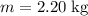 block. In other words, this block is moving backwards towards the incline after the collision.
block. In other words, this block is moving backwards towards the incline after the collision.