Question

The focus of a parabola is
`(0, 2)`, and its directrix is the vertical line
`x=-6`. Identify the axis of symmetry, the vertex, and the direction the parabola opens.

Answer 1

`\huge\boxed{\text{Axis of Symmetry: } y = 2}`

`\huge\boxed{\text{Vertex: } (-3, 2)}`

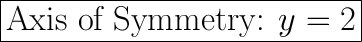
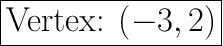
The parabola opens to the right (horizontally)

Explanation:

We need to note a few basic rules about focuses and directrix’s of a parabola.

1. The directrix never touches the parabola, however it is perpendicular to the axis of symmetry

2. The focus never touches the parabola, however it lies on the axis of symmetry of the parabola

3. The directrix is always the same distance away from the vertex as the focus

If we know that the focus of the parabola is (0, 2) and the directrix lies on x=-6. that means these points are 6 units apart as we can assume the line x = -6 crosses the point (-6, 2), making these points 6 units apart (since |-6 - 0| = 6)

These are 6 points apart horizontally, via the x-axis, meaning that this is a horizontally facing parabola, and it opens to the right. We know it can’t open to the left because then the directrix (x = -6) would touch the parabola and then it wouldn’t be a directrix!

The vertex of the parabola will be the same distance away from the focus and the directrix. Since these are 6 units apart, that means the focus will lie
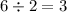`6 / 2 = 3` units away from either one.

Halfway between 0 and -6 is -3, so we know the vertex lies on x-coordinate -3. We also know that the focus is on y-value 2, meaning that the vertex will also be on y = 2, since the focus is always on the axis of symmetry.

So our vertex is at
`(-3, 2)`.

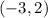We know that this is a horizontally facing parabola, meaning that our axis of symmetry is going to lay on a y coordinate. The axis of symmetry always contains the vertex, so that means that we can just take the y value of the vertex and use that as the axis of symmetry. The vertex lies at y value 2, meaning that the axis of symmetry is
`y=2`

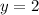
In conclusion

• The vertex is at
  `(-3, 2)`
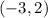
• The axis of symmetry is at
  `y=2`
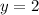
• The parabola opens to the right (horizontally)

Hope this helped!