Question

Newton’s Law of Cooling. Newton’s law of cooling states that the rate of change in the temperature T(t) of a body is proportional to the difference between the temperature of the medium M(t) and the temperature of the body. That is, dT/dt = K[M(t) - T(t)] , where K is a constant. Let K = 0.04 (min)-1 and the temperature of the medium be constant, M(t) = 293 kelvins. If the body is initially at 360 kelvins, use Euler’s method with h = 3.0 min to approximate the temperature of the body after

(a) 30 minutes.

(b) 60 minutes.

Answer 1

After 30 minutes, the temperature of the body is: T₁₀ = 311.60 K

After 60 minutes, the temperature of the body is: T₂₀ = 298.18 K

Step-by-step explanation:

Given that:

`(dT)/(dt)= K \bigg [ M(t) -T(t)\bigg]`

where;

K = 0.04

M(t) = 293

Then;

`(dT)/(dt)= 0.04 \bigg [ 293 -T\bigg]`

`(dT)/(dt)= 11.72 -0.04 \ T`

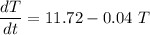
Using Euler's Formula;

`T_(n+1) = T_n + hf( t_n, T_n)`

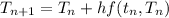
where;

`f(t_n,T_n) = 11.72 - 0.04 T_n`

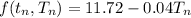
Then;

`T_(n+1) = T_n + 3.0 (11.72-0.04 \ T_n)`

`T_(n+1) = 0.88T_n + 35.16 \ ---(1)`

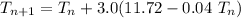
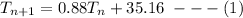
At initial state
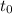`t_0` (0);
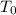`T_0` = 360

At t₁ = 3.0 when T₀ = 360

`T_1= 0.88 T_o + 35.16`

`T_1= 0.88 (360) + 35.16`

`T_1 = 351.96 \ K`

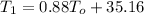
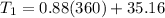
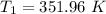
At t₂ = 6.0 when T₂ = 0.88T₁ + 35.16

T₂ = 0.88(351.96) + 35.16

T₂ = 344.89 K

At t₃ = 9.0 when T₃ = 0.88T₂ + 35.16

T₃ = 0.88(344.89) + 35.16

T₃ =338.66 K

At t₄ = 12.0 when T₄ = 0.88T₃ + 35.16

T₄ = 0.88(338.66) + 35.16

T₄ = 333.18 K

At t₅ = 15.0 when T₅ = 0.88T₄ + 35.16

T₅ = 0.88(333.18) + 35.16

T₅ = 328.36 K

At t₆ = 18.0 when T₆ = 0.88T₅ + 35.16

T₆ = 0.88(328.36) + 35.16

T₆ = 324.12 K

At t₇ = 21.0 when T₇ = 0.88T₆ + 35.16

T₇ = 0.88(324.12) + 35.16

T₇ = 320.39 K

At t₈ = 24.0 when T₈ = 0.88T₇ + 35.16

T₈ = 0.88(320.29) + 35.16

T₈ = 317.02 K

At t₉ = 27.0 when T₉ = 0.88T₈ + 35.16

T₉ = 0.88(317.02) + 35.16

T₉ = 314.14 K

At t₁₀ = 30 when T₁₀ = 0.88T₉ + 35.16

T₁₀ = 0.88(314.14) + 35.16

T₁₀ = 311.60 K

At t₁₁ = 33.0 when T₁₁ = 0.88T₁₀ + 35.16

T₁₁ = 0.88(311.60) + 35.16

T₁₁ = 309.37 K

At t₁₂ = 36.0 when T₁₂ = 0.88T₁₁ + 35.16

T₁₂ = 0.88(309.37)+ 35.16

T₁₂ = 307.41 K

At t₁₃ = 39.0 when T₁₃ = 0.88T₁₂ + 35.16

T₁₃ = 0.88( 307.41) + 35.16

T₁₃ = 305.68 K

At t₁₄ = 42.0 when T₁₄ = 0.88T₁₃ + 35.16

T₁₄ = 0.88(305.68) + 35.16

T₁₄ = 304.16 K

At t₁₅ = 45.0 when T₁₅ = 0.88T₁₄ + 35.16

T₁₅ = 0.88(304.16) + 35.16

T₁₅ = 302.82 K

At t₁₆ = 48.0 when T₁₆ = 0.88T₁₅ + 35.16

T₁₆ = 0.88(302.82) + 35.16

T₁₆ = 301.64 K

At t₁₇ = 51.0 when T₁₇ = 0.88T₁₆ + 35.16

T₁₇ = 0.88(301.64) + 35.16

T₁₇ = 300.60 K

At t₁₈ = 54.0 when T₁₈ = 0.88T₁₇ + 35.16

T₁₈ = 0.88(300.60) + 35.16

T₁₈ = 299.69 K

At t₁₉ = 57.0 when T₁₉ = 0.88T₁₈ + 35.16

T₁₉ = 0.88(299.69) + 35.16

T₁₉ = 298.89 K

At t₂₀ = 60 when T₂₀ = 0.88T₁₉ + 35.16

T₂₀ = 0.88(298.89) + 35.16

T₂₀ = 298.18 K