Question

Snow Dome Ski Resort has 65 inches of snow. It is currently snowing there at a rate of 1 inch per hour. Mt. Winterpark Ski Resort has 74 inches of snow. Currently it is snowing there at a rate of ½ inch per hour.

a) Write equations that show the amount of snow at each resort as a function of the number of hours of snow.

b) If the snow continues at this rate, when will Snow Dome have more snow than Mt. Winterpark? Show your solution process clearly.

Answer 1

a) Equation for Snow Dome Ski Resort:

`I_s = 65+t`

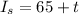
Equation for Mt. Winterpark Ski Resort:

`I_m = 74+(t)/(2)`

b) After 19 hours, Snow dome will have more snow.

Explanation:

Given that:

Initial snow at Snow Dome Ski Resort = 65 inches

Snowing rate at Snow Dome Ski Resort = 1 inch per hour

Initial snow at Mt. Winterpark Ski Resort = 74 inches

Initial snow at Mt. Winterpark Ski Resort =
`(1)/(2)` inch per hour

a) To write equations that show amount of snow at each resort.

Let the time in hours be represented by
`t`.

Snow increased in
`t` hours by snowing at Snow Dome Ski Resort =
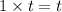`1* t = t` inches per hour

Snow increased in
`t` hours by snowing at Mt. Winterpark Ski Resort =
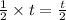`(1)/(2)* t = (t)/(2)` inches per hour

Equation for Snow Dome Ski Resort:

`I_s = 65+t`

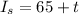
Equation for Mt. Winterpark Ski Resort:

`I_m = 74+(t)/(2)`

b) Time at which Snow Dome has more snow.

Using the above equations, we can write the following inequality:

`65+t>74+(t)/(2)\\\Rightarrow t-(t)/(2)>74-65\\\Rightarrow (t)/(2)>9\\\Rightarrow t>18\ hours`

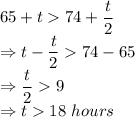
After 18 hours have passed, they will have equal amount of snow.

After 19 hours, Snow dome will have more snow.