Question

A student, starting from rest, slides down a water slide. On the way down, a kinetic frictional force (a nonconservative force) acts on her. The student has a mass of 71.0 kg, and the height of the water slide is 12.7 m. If the kinetic frictional force does -5.10 103 J of work, how fast is the student going at the bottom of the slide

Answer 1

`10.27m/s`

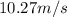
Step-by-step explanation:

Given data

work W= -5.10 10^3 J

mass m= 71kg

final height of slide h2= 12.7m

initial height of slide h1=0m

initial velocity v1= 0m/s

final velocity v2=?

Step two:

required

Final velocity

The work-energy theorem is expressed as'

`W=1/mv_2^2 +mgh_2-(1/mv_1^2+mgh_1)`

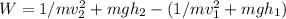
make V2 subject of formula we have final speed

`v_2=\sqrt{(2W)/(m)+v_1^2-2g(h_1-h_2) } \\\\`

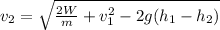
substitute our given data we have

`v_2=\sqrt{(2*(-5.1*10^3))/(71)+0^2-2*9.81(12.7) } \\\\v_2=√(143.66-249.174 ) \\\\v_2=√(105.514 ) \\\\v_2=10.27m/s`

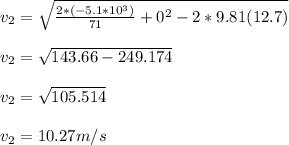
The student going at 10.27m/s