Question

Solve the equation. If exact roots cannot be found, state the consecutive integers between which the roots are located.

x = -3 and 1
x = -2
No real roots.
x = 3 and -1

Answer 1

No real roots.

General Formulas and Concepts:

Pre-Algebra

• Order of Operations: BPEMDAS

Algebra I

• Standard Form: ax² + bx + c = 0
• Quadratic Formula:
  `x=(-b\pm√(b^2-4ac) )/(2a)`

Algebra II

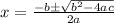
• Imaginary Roots: √-1 = i

Explanation:

Step 1: Define

-3x² + 2x = 1

Step 2: Rewrite in Standard Form

1. Subtract 1 on both sides: -3x² + 2x - 1 = 0

Step 3: Define

a = -3

b = 2

c = -1

Step 4: Find roots

1. Substitute in variables:
   `x=(-2\pm√(2^2-4(-3)(-1)) )/(2(-3))`
2. Exponents:
   `x=(-2\pm√(4-4(-3)(-1)) )/(2(-3))`
3. Multiply:
   `x=(-2\pm√(4-12) )/(-6)`
4. Subtract:
   `x=(-2\pm√(-8) )/(-6)`

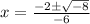
Here we see that we cannot take the square root of a negative number. We will get no real roots and only imaginary ones.