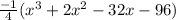The graph in the question is missing.
Answer:
y =
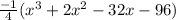
Explanation:
The function is cubic
It has roots as -4, -4 , 6
this means the value of x = -4, -4 , 6 which makes the entire equation zero
so we have solutions as
x+4 = 0
x+4 = 0
x- 6 = 0
on forming a cubic equation using these
(x+4)(x+4)(x-6)
the equation passes through (2,36)
put x = 2
(2+4)(2+4)(2-6) = (6)*(6)*(-4)
which exceeds 36 so we product the equation with -1/4 to get 36
Final equation
y =
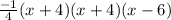
y =