Question

HELP IT'S DUE IN 18 MINUTES!

Answer 1

Please check the explanation!

Explanation:

As the discrimination expression is

`b^2-4ac`

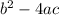
if

`b^2-4ac\:<0`

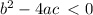
then the equation has no real solution.

Given the equation

`mx^2+3x+1-m=0`

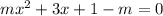
by comparing the quadratic equation

`\:ax^2+bx+c=0`

`mx^2+3x+1-m=0`

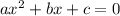
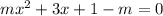
we can observe that

`a=m`

`b=3`

`c=(1-m)`

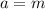
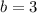
substituting the values in discrimination to find the values of m

so

`3^2-4m\left(1-m\right)=0`

`9-4m+4m^2=0`

`4m^2-4m+9=0`

`(-4m+4m^2)/(4)=(-9)/(4)`

`-m+m^2=-(9)/(4)`

`\left(m-(1)/(2)\right)^2=-2`

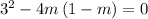
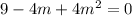
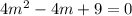
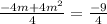
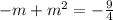
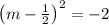
as

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

so solving

`m-(1)/(2)=√(-2)`

`m-(1)/(2)=√(-1)√(2)`

`m-(1)/(2)=√(2)i` ∵
`√(-1)=i`

`m=√(2)i+(1)/(2)`

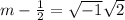
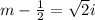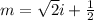
and also solving

`m-(1)/(2)=-√(-2)`

`m-(1)/(2)=-√(2)i`

`m=-√(2)i+(1)/(2)`

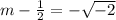
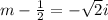
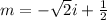
As we know that

if

`b^2-4ac\:<0`

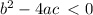
then the equation has no real solution.

Therefore, for the values of
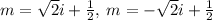`m=√(2)i+(1)/(2),\:m=-√(2)i+(1)/(2)`, for which the equation
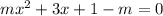`mx^2+3x+1-m=0` will have no solution.