Displacement of the airplane (s) = 2000 m
Initial velocity of the airplane (u) = 0 m/s (Starts from rest)
Final velocity of the airplane = 56.4 m/s
Equation used to solve the problem:
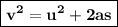
By substituting values in the equation, we get:
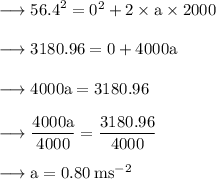
 Minimum uniform acceleration necessary for the plane to take flight (a) = 0.80 m/s²
Minimum uniform acceleration necessary for the plane to take flight (a) = 0.80 m/s²