Question

PLS PLS PLS PLS PLS I GIVE ALL MAH POINTS

Answer 1

125 = 5³, and the given expression reduces to

`\left(√(125)\right)^(\frac13)\cdot\left(\sqrt[3]{125}\right)^(\frac12)=\left(125^(\frac12)\right)^(\frac13)\cdot\left(125^(\frac13)\right)^(\frac12)=125^(\frac16)\cdot125^(\frac16)=125^(\frac13)`

so it has a value of 5.

Now:

• the first choice is equivalent, since 625 = 25², so

`\frac{\sqrt[3]{625}}{5^(\frac13)}=(25^(\frac23))/(5^(\frac13))=(5^(\frac43))/(5^(\frac13))=5`

• the second choice is not equivalent, since

`5 \cdot 25^(\frac13) = 5 \cdot 5^(\frac23) = 5^(\frac43)`

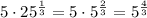
• the third choice is also equivalent, since

`\frac{\left(\sqrt[4]{5}\right)^7}{125^(\frac14)}=(5^(\frac74))/(5^(\frac34))=5`

• the fourth choice is also equivalent, since

`\frac{5^(\frac12)\cdot25^(\frac13)}{\sqrt[6]{5}}=(5^(\frac12)\cdot5^(\frac23))/(5^(\frac16))=(5^(\frac76))/(5^(\frac16))=5`