Answer:
Question 32
- Scale Factor = 3/8
- Ratio of Perimeters = 8 : 3
- Ratio of Areas = 64 : 9
- Area of smaller figure = 144 mm²
Question 33
- Scale Factor = 10/7
- Ratio of Perimeters = 7 : 10
- Ratio of Areas = 49 : 100
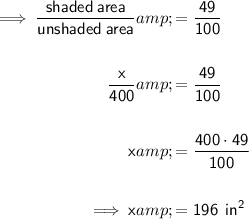
- Area of smaller figure = 196 in²
Explanation:
Scale Factor: A number used as a multiplier when scaling an object.
Perimeter: The total distance around the outside of a 2D shape.
Area: The space occupied by a flat shape, measured in two dimensions.
Question 32
Scale Factor
To find the scale factor from the shaded figure to the unshaded figure, divide the given side length of the unshaded figure by the given side length of the shaded figure:
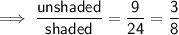
Ratio of Perimeters
Perimeters are measured in one dimension (length). To find the ratio of the perimeters, divide the given side length of one figure by the given side length of the other:
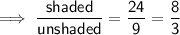
Therefore:

Ratio of Areas
Area is measured in two dimensions. To find the ratio of the areas, divide the square of the given side length of one figure by the square of the given side length of the other:
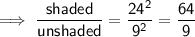
Therefore:
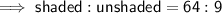
Area of the smaller figure (unshaded)
Area of shaded figure = 1024 mm²
Let x = area of unshaded figure
Use the ratio found above:

Question 33
Scale Factor
To find the scale factor from the shaded figure to the unshaded figure, divide the given side length of the unshaded figure by the given side length of the shaded figure:

Ratio of Perimeters
Perimeters are measured in one dimension (length). To find the ratio of the perimeters, divide the given side length of one figure by the given side length of the other:
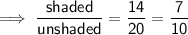
Therefore:
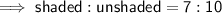
Ratio of Areas
Area is measured in two dimensions. To find the ratio of the areas, divide the square of the given side length of one figure by the square of the given side length of the other:
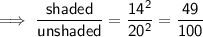
Therefore:
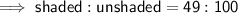
Area of the smaller figure (shaded)
Area of unshaded figure = 400 in²
Let x = area of shaded figure
Use the ratio found above: