Answer:
Approximately
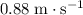 to the right (assuming that both astronauts were originally stationary.)
to the right (assuming that both astronauts were originally stationary.)
Step-by-step explanation:
If an object of mass
 is moving at a velocity of
is moving at a velocity of
 , the momentum
, the momentum
 of that object would be
of that object would be
 .
.
Since momentum of this system (of the astronauts) conserved:
 .
.
Assuming that both astronauts were originally stationary. The total initial momentum of the two astronauts would be
 since the velocity of both astronauts was
since the velocity of both astronauts was
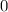 .
.
Therefore:
 .
.
The final momentum of the first astronaut (
 ,
,
 to the left) would be
to the left) would be
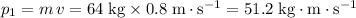 to the left.
to the left.
Let
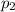 denote the momentum of the astronaut in question. The total final momentum of the two astronauts, combined, would be
denote the momentum of the astronaut in question. The total final momentum of the two astronauts, combined, would be
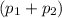 .
.
 .
.
Hence,
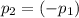 . In other words, the final momentum of the astronaut in question is the opposite of that of the first astronaut. Since momentum is a vector quantity, the momentum of the two astronauts magnitude (
. In other words, the final momentum of the astronaut in question is the opposite of that of the first astronaut. Since momentum is a vector quantity, the momentum of the two astronauts magnitude (
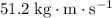 ) but opposite in direction (to the right versus to the left.)
) but opposite in direction (to the right versus to the left.)
Rearrange the equation
 to obtain an expression for velocity in terms of momentum and mass:
to obtain an expression for velocity in terms of momentum and mass:
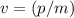 .
.
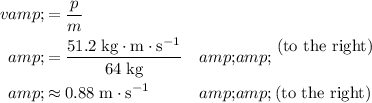 .
.
Hence, the velocity of the astronaut in question (
 ) would be
) would be
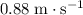 to the right.
to the right.