Question

Evaluate triple integral ​

Answer 1

`\\ (1)/(8) e^(4a)-(3)/(4)e^(2a)+e^(a) -(3)/(8) \\\\or\\\\ (e^(4a)-6e^(2a)+8e^(a)-3)/(8)`

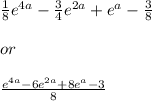
Explanation:

`\\ \int\limits^(a)_(0) \int\limits^(x)_(0) \int\limits^(x+y)_(0) {e^(x+y+z)} \, dzdydx \\\\=\int\limits^(a)_(0) \int\limits^(x)_(0) [\int\limits^(x+y)_(0) {e^(x+y)e^z} \, dz]dydx \\\\\\=\int\limits^(a)_(0) \int\limits^(x)_(0) [e^(x+y)\int\limits^(x+y)_(0) {e^z} \, dz]dydx\\\\=\int\limits^(a)_(0) \int\limits^(x)_(0) [e^(x+y)e^z\Big|_0^(x+y)]dydx \\\\\\=\int\limits^(a)_(0) \int\limits^(x)_(0) [e^(x+y)e^(x+y)-e^(x+y)]dydx \\\\\\=\int\limits^(a)_(0) \int\limits^(x)_(0) e^(2x+2y)-e^(x+y)dydx \\\\\\`

`\\=\int\limits^(a)_(0) [\int\limits^(x)_(0) e^(2x)e^(2y)-e^(x+y)dy]dx \\\\\\=\int\limits^(a)_(0) [\int\limits^(x)_(0) e^(2x)e^(2y)dy- \int\limits^(x)_(0)e^(x)e^(y)dy]dx \\\\\\u=2y\\du=2dy\\dy=(1)/(2)du\\\\\\=\int\limits^(a)_(0) [(e^(2x))/(2)\int e^(u)du- e^x\int\limits^(x)_(0)e^(y)dy]dx \\\\\\=\int\limits^(a)_(0) [(e^(2x))/(2)\cdot e^(2y)\Big|_0^x- e^xe^(y)\Big|_0^x]dx \\\\\\=\int\limits^(a)_(0) [(e^(2x+2y))/(2) - e^(x+y)\Big|_0^x]dx \\\\`

`\\=\int\limits^(a)_(0) [(e^(4x))/(2) - e^(2x)-(e^(2x))/(2) + e^(x)]dx \\\\\\=\int\limits^(a)_(0) (e^(4x))/(2) -(3e^(2x))/(2) + e^(x)dx \\\\\\=\int\limits^(a)_(0) (e^(4x))/(2)dx -\int\limits^(a)_(0)(3e^(2x))/(2)dx + \int\limits^(a)_(0)e^(x)dx \\\\\\u_1=4x\\du_1=4dx\\dx=(1)/(4)du_1\\\\\u_2=2x\\du_2=2dx\\dx=(1)/(2)du_2\\\\\\=(1)/(8)\int e^(u_1)du_1 -(3)/(4)\int e^(u_2)du_2 + \int\limits^(a)_(0)e^(x)dx \\\\\\`

`\\=(1)/(8)e^(u_1)\Big| -(3)/(4)e^(u_2)\Big| + e^(x)\Big|_0^a \\\\\\=(1)/(8)e^(4x)\Big|_(0)^a -(3)/(4)e^(2x)\Big|_(0)^a + e^(x)\Big|_0^a \\\\\\=(1)/(8)e^(4x) -(3)/(4)e^(2x) + e^(x)\Big|_0^a \\\\\\=(1)/(8)e^(4a) -(3)/(4)e^(2a) + e^(a)-(1)/(8) +(3)/(4) -1\\\\\\=(1)/(8)e^(4a) -(3)/(4)e^(2a) + e^(a)-(3)/(8)\\\\\\`

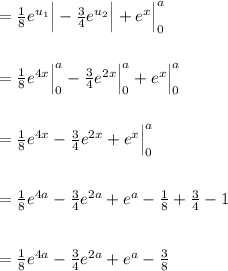
Sorry if that took a while to finish. I am in AP Calculus BC and that was my first time evaluating a triple integral. You will see some integrals and evaluation signs with blank upper and lower boundaries. I just had my equation in terms of u and didn't want to get any variables confused. Hope this helps you. If you have any questions let me know. Have a nice night.