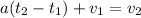Question

Please at least help me cause I have no idea

Solve for v2

`a \: ave = (v2 - v1)/(t2 - t1)`
​

Answer 1

Solving the given formula for v2 gives us:

`a(t_2-t_1)+v_1 = v_2`

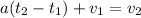
Explanation:

Solving an equation for a particular variable means that the variable has to be isolated on one side of the equation.

Given equation is:

`a = (v_2-v_1)/(t_2-t_1)`

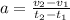
Multiplying both sides by t2-t1

`(t_2-t_1) . a = (v_2-v_1)/(t_2-t_1) . (t_2-t_1)\\a(t_2-t_1) = v_2-v_1`

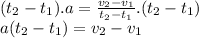
Adding v1 to both sides of the equation

`a(t_2-t_1)+v_1 = v_2-v_1+v_1\\a(t_2-t_1)+v_1 = v_2`

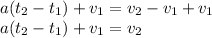
Hence,

Solving the given formula for v2 gives us:

`a(t_2-t_1)+v_1 = v_2`