Question

a small airplane flies 1 015miles with an average speed of 290 mph. 1.75 hours after the plane leaves, a Boeing 747 leaves from the same point. Both planes arrive at the same time; what was the average speed of Boeing 747?

Answer 1

The Boeing 747 had an average speed of 580 mph.

Explanation:

Constant speed motion

An object is said to travel at constant speed if the ratio of the distance traveled by the time taken is constant.

Expressed in a simple equation, we have:

`\displaystyle v=(d)/(t)`

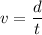
Where

v = Speed of the object

d = Distance traveled

t = Time taken to travel d.

From the equation above, we can solve for d:

d = v . t

And we can also solve it for t:

`\displaystyle t=(d)/(v)`

The small airplane travels 1015 miles at a constant speed of v=290 miles/hour. The time it took to arrive its destiny was:

`\displaystyle t=(1015)/(290)`

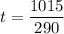
t = 3.5 hours

The Boeing 747 left from the same point 1.75 hours after the small plane and traveled the same distance. It needed a time t' = 3.5 - 1.75 = 1.75 hours, thus its speed must have been:

`\displaystyle v=(1015)/(1.75)=580`

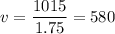
The Boeing 747 had an average speed of 580 mph.