Answer:
M(13)=14.3 gram
Explanation:
Exponential Decay Function
The exponential function is used to model natural decaying processes, where the change is proportional to the actual quantity.
An exponential decaying function is expressed as:
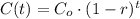
Where:
C(t) is the actual value of the function at time t
Co is the initial value of C at t=0
r is the decaying rate, expressed in decimal
The element has an initial mass of Mo=970 grams, the decaying rate is r=27.7% = 0.277 per minute.
The equation of the model is:
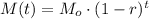
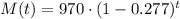
Operating:
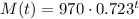
After t=13 minutes the remaining mass is:
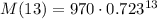
Calculating:
M(13)=14.3 gram