Question

Three persons wants to push a wheel cart in the direction marked x in Fig. The two person push with horizontal forces F1 and F2 as F1 = 45 N 70degree And F2 = 75 N , 20 Degree (a) Find the magnitude and direction of the force that third person should exert to stop this cart. You can ignore the effects of friction. (b) If the third person exerts the force found in part (a), the cart accelerates at 200 m/S2 in the (+) x-direction. What is the weight of the cart​

Answer 1

I had to search the Figure on Google to solve this question.

a) The magnitude of the force F₃ is:

`F_(3) = 87.47 N`

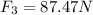
And the direction of F₃:

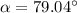`\alpha = 79.04 ^(\circ)` (with respect to the y-direction, in the third quadrant)

b) P = 4.22 N

Step-by-step explanation:

I had to search the Figure on Google to solve this question.

a) We can find the force of the third person as follows:

`\Sigma F_(x) = F_(1x) + F_(2x) + F_(3x) = 0`

`\Sigma F_(y) = F_(1y) - F_(2y) + F_(3y) = 0`

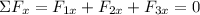
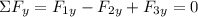
So, in x-direction we have:

`\Sigma F_(x) = 45 N*cos(70) + 75 N*cos(20) + F_(3x) = 0`

`F_(3x) = -85.87 N`

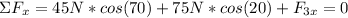
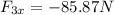
In y-direction we have:

`\Sigma F_(y) = 45 N*sin(70) - 75 N*sin(20) + F_(3y) = 0`

`F_(3y) = -16.63 N`

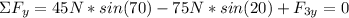
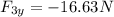
The magnitude of the force F₃ is:

`F_(3) = \sqrt{F_(3x)^(2) + F_(3y)^(2)} = \sqrt{(-85.87 N)^(2) + (-16.63 N)^(2)} = 87.47 N`

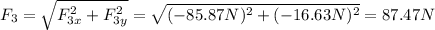
To find the direction of F₃ we need to calculate its angle with respect to the y-direction (in the third quadrant):

`tan(\alpha) = (|F_(3x)|)/(|F_(3y)|) = (85.87 N)/(16.63 N)`

`\alpha = 79.04 ^(\circ)`

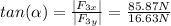
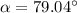
b) If the third person exerts the force found in part (a) the car will stop, so the only way for the cart to accelerate at 200 m/s² is that the third person does not exert the force found in a.

To find the weight of the cart​ when it accelerates at 200 m/s², we need to consider: F₃ = 0.

First, we need to find the cart's mass. Since the car is moving in the x-direction we have:

`\Sigma F_(x) = F_(1x) + F_(2x) = ma`

`45 N*cos(70) + 75 N*cos(20) = m*200 m/s^(2)`

`m = (45 N*cos(70) + 75 N*cos(20))/(200 m/s^(2)) = 0.43 kg`

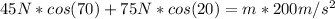
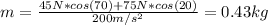
Now, the weight of the cart​ is:

`P = mg = 0.43 kg*9.81 m/s^(2) = 4.22 N`

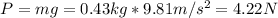
I hope it helps you!