Question

Una recta que pasa por los puntos A (2,1) y B (6,3) y otra recta pasa por A y por el punto (0,y) ¿Cuánto vale y, si ambas rectas son perpendiculares?

Answer 1

The translation of the question given is

A line that passes through the points A (2,1) and B (6,3) and another line passes through A and through the point (0, y). What is y worth, if both lines are perpendicular?

Answer:

y = 5

Explanation:

Line 1 that passes through A (2,1) and B (6,3)

Slope (m1) = 3-1/6-2 = 2/4 = 1/2

y - 1 =
`(1)/(2)` ( x -2)

2y - 2 = x- 2

y =
`(x)/(2)`

Line 2 passes through A (2,1) and (0,y)

slope (m2) =
`(y-1)/(-2)`

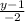
Line 1 and Line 2 are perpendicular

m1*m2 = -1

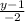`(1)/(2)` *
`(y-1)/(-2)` = -1

y-1 = 4

y = 5

slope = -2

Equation of Line 2

Y-1 = -2(x-2)

y -1 = -2x +4

2x +y = 5