Complete the square in the denominator:
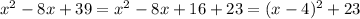
Then in the integral, substitute
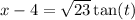 and
and
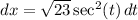 .
.
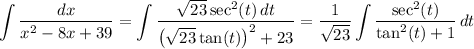
Recall that tan²(x) + 1 = sec²(x) for all x (such that cos(x) ≠ 0, anyway). Then the integral reduces to the trival
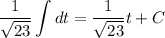
and putting the result back in terms of x, we get
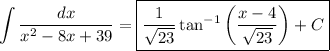
If you want to proceed via partial fractions, there's more work involved. We can use the complete-square expression to easily find the roots of the denominator:
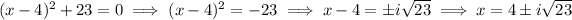
Then we factorize
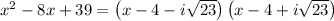
and the PFD would be
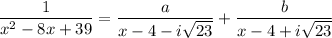
Solve for the coefficients:
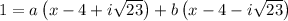
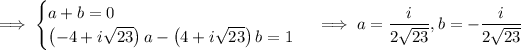
Then the integral is
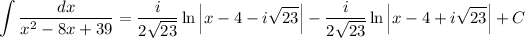
and we can condense the logarithms to
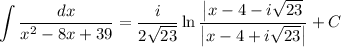
Now we fight the urge to be discouraged by the presence of imaginary numbers in this result. The two antiderivatives are one and the same!
For any complex number z, the following identity holds:
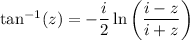
With some rewriting, we have for instance
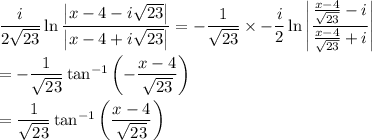
Admittedly, I skip over a bunch of details, but the point is that both methods end with the same result, but the first method is much simpler to follow and execute, in my opinion.