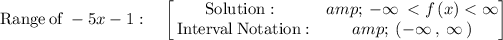Question

Find the domain and range of y=-5x-1

Answer 1

The domain and range of the linear equation y = -5x - 1 are both all real numbers, represented as (-∞, ∞).

Step-by-step explanation:

• The question asks to find the domain and range of the linear equation y = -5x - 1.
• The domain of a linear equation is all the values that x can take, which, in this case, is all real numbers because there are no restrictions on x in the equation.
• Hence, the domain is (-∞, ∞).
• The range consists of all the possible values of y.
• Since this is a non-horizontal linear equation, y can take any real value depending on the value of x, so the range is also all real numbers, or (-∞, ∞).

Answer 2

• 
  `\mathrm{Domain\:of\:}\:-5x-1\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<x<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`

• 
  `\mathrm{Range\:of\:}-5x-1:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<f\left(x\right)<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`

Step-by-step explanation:

Finding the domain:

The domain of a function is the set of possible input values for which the function is real and defined.

Given the function

`y=-5x-1`

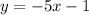
The function has no undefined points nor domain constraints. Hence, the domain is

`-\infty \:<x<\infty \:`

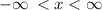
i.e.

`\mathrm{Domain\:of\:}\:-5x-1\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<x<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`

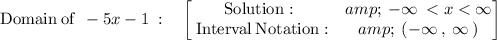
Finding the range:

The range of a function is the set of possible output values (dependent variable y values) for which a function is defined.

The range of polynomials with odd degree is all the real numbers.

Hence, the domain is

`-\infty \:<y<\infty \:`

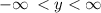
i.e.

`\mathrm{Range\:of\:}-5x-1:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<f\left(x\right)<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`