Answer:
angle XOY =
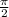 (in radians) or 90° (in degrees)
(in radians) or 90° (in degrees)
Explanation:
So firstly we need to consider that the unit of measurement is radians, not degrees, as represented by the 'measures 16π cm'.
Next, since we have the length of arc XY given as 16π cm, we can apply the formula for the length of an arc, in radians, which is
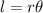 .
.
I'm assuming that you know how to derive the formula for arc length since you are getting questions about arc length like this, but if not, then you can just search on the internet: "derivation for the formula of arc length in radians"
Therefore: we should let ∠XOY = ∅ and so,
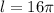 and
and
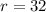
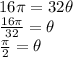
∴∠XOY =
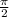 radians
radians
(Unless otherwise stated, return your answer in the same unit of measurement as the measurements in the question)