Question

A motorcycle starts from rest and maintains a constant acceleration whose magnitude is 0.45 m/s².

a) Calculate how long it will take to travel a distance of 1.6 km.
b) How fast will it be in this time in m/s and in km/h?

Answer 1

a) If the motorcycle starts from rest, then we have an initial speed equal to zero (V0 = 0), with this we can choose a formula that does not contain the initial speed, now we also know that what it asks us is the time that it takes a certain speed to pass, so the formula we will use will be:

`\bf{\displaystyle d=\frac{a{{t}^(2)}}{2}}`

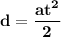
Clearing "t"

`\boldsymbol{\sf{t=\sqrt{(2d)/(a) } } }`

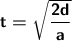
The distance is in Kilometers, we first need to pass this distance in meters, so we'll need to do our conversion:

`\boldsymbol{\sf{1.6\\ot{km}*\frac{1000 \ m}{1\\ot{km}}=1600 \ m } }`

1.6 km = 1600m

Substituting our data into the formula:

`\boldsymbol{\sf{t=\sqrt{(2d)/(a) }=\sqrt{(2(1600 \ m) )/(9.45 \ (m)/(s^2) ) }=84.32 \ s } }`

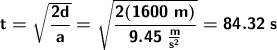
So the motorcycle will take 84.32 seconds to travel 1600 meters.

b) Since we are asked to obtain the speed in the time it took for the 1600 meters, we are going to use the following formula.

`\boldsymbol{\sf{V_(f)=at }}`

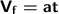
Substituting our data:

`\boldsymbol{\sf{V_(f)=at=\left(0.45 \ \frac{m}{\\ot{s^(2)} }\right)(84.23 \ s)=37.94 \ (m)/(s) }}`

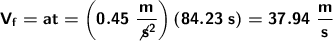
In order to express the final result of the speed, in terms of km/h, we would only apply the conversion factors.

`\boldsymbol{\sf{V_(f)=37.94\frac{\\ot{m}}{\\ot{s}}*\frac{1 \ km}{1000\\ot{m}}*\frac{3600\\ot{s}}{1 \ h}=136.58 \ (km)/(h) }}`