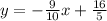Question

Write the equation of the line that passes through the points (8, -4) and (-2,5).

Put your answer in fully reduced point-slope form, unless it is a vertical or horizontal
line.

Answer 1

The equation in the slope-intercept form will be:

Explanation:

Given the points

• (8, -4) and (-2, 5)

The slope between two points

`m=(5-\left(-4\right))/(-2-8)`

`m=-(9)/(10)`

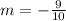
As the point-slope form is

`y-y_1=m\left(x-x_1\right)`

substituting the values m = -9/10 and (8, -4)

`y-\left(-4\right)=-(9)/(10)\left(x-8\right)`

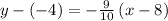
Writing the line equation in the slope-intercept form

`y=mx+b`

where m is the slope and b is the y-intercept

so the equation in the slope-intercept form will be:

`y-\left(-4\right)=-(9)/(10)\left(x-8\right)`

`y+4=-(9)/(10)\left(x-8\right)`

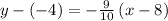
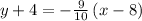
subtract 4 from both sides

`y+4-4=-(9)/(10)\left(x-8\right)-4`

`y=-(9)/(10)x+(16)/(5)`

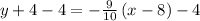
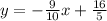
Therefore, the equation in the slope-intercept form will be:

`y=-(9)/(10)x+(16)/(5)`