Answer:
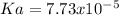
Step-by-step explanation:
Hello!
In this case, since the pH is measure of the amount of hydrogen ions in solution, first given the pH we can compute the concentration of hydrogen ions via:
![pH=-log([H^+])](https://img.qammunity.org/2021/formulas/chemistry/college/80k0jnij8v7qd0dtehezpuvp9exa33y466.png)
![[H^+]=10^(-pH)=10^(-2.353)=4.436x10^(-3)M](https://img.qammunity.org/2021/formulas/chemistry/college/atbx2pm6ysh5b4wclqp9t9jy0tdi7cee1w.png)
Thus, since the ionization of the given acid, leads to the following equilibrium expression as it is a weak one:
![Ka=([H^+][A^-])/([HA])](https://img.qammunity.org/2021/formulas/chemistry/college/kzt7pcnoonz2fwfrgadywivsijtflo2dmk.png)
We notice the concentration of hydrogen ions equal the concentration of the acids conjugate base, so we can compute:
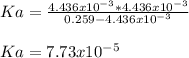
Best regards!