Given:
Height of box = (x-2)
Volume of box =
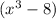
To find:
The expression for the base area.
Solution:
We know that,
Volume of a box(V) = Base area(B) × Height(h)
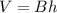
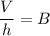
On substituting the given values, we get
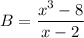
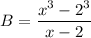
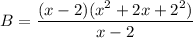
![[\because a^3-b^3=(a-b)(a^2+ab+b^2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/42ppvii6ssdvpd5j3onja5p0xmvlvpe0yp.png)
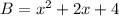
So, the base area is
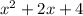 .
.
Therefore, the correct option is B.