This problem implies more cases to solve as well as the use of other formulas that we can use in the subject of free fall, if we read our exercise again, we will realize that we only have a height of 150 meters from where it is dropped freely a ball. To proceed to resolve, we collect the data.
- Distance descended at 4 seconds
- What speed does it have at 4 seconds?
- How far does it take to reach the ground?
Data:
h = 150 m
g = 9.8 m/s²
a) Obtain the distance at 4 seconds when the ball descends
In order to obtain the distance traveled in 4 seconds, we can use the following formula:
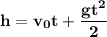
Remember, that as it is a free fall, the initial speed is null, that is, zero. So the formula reduces:
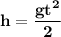
We are going to place the 4 seconds in the “t” of time. Thus:
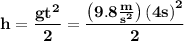
Carrying out the indicated operations:
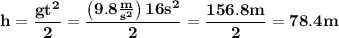
That is to say that the height at 4 seconds is 78.4 meters.
b) What speed will it have after 4 seconds?
For the velocity at 4 seconds, we use the following formula:
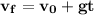
Remember, that since there is no initial speed because it is free fall, then the formula is reduced:
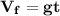
Substituting our data and calculating:
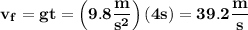
So the speed at 4 seconds is 39.2 m/s.
c) Distance it takes to reach the ground.
Although it seems difficult to solve this section, it is not. It's very easy, let's remember that after 4 seconds it has traveled 78.4 meters and that the height from where the ball was dropped is 150 meters, so the difference is the amount that remains to reach the ground, that is:

It is as if we had:
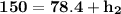
Clearing "h2" what would be the distance to reach the ground.
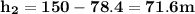
In other words, we need to travel 71.6 meters to reach the ground.