Question

May anyone please help. it will mean alot to me ​

Answer 1

`\underline{\underline{ \huge{ \bf{Answer}}}}`

`\sf`

`1.\bf \quad(m + 11)(m - 11)`

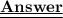
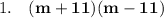
Using the algebraic identity :

`\sf(a + b)(a - b) = {a}^(2) - {b}^(2)`

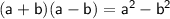
Therefore,

`\sf \longrightarrow \: {m}^(2) - {11}^(2)`

`\sf \longrightarrow \: {m}^(2) - 121`

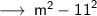
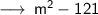
i.e Product of sum and difference.

___________________________________

`\bf 2. \quad(y + 12)(y - 5)`

`\sf \longrightarrow \: y(y - 5) + 12(y - 5)`

`\sf \longrightarrow \: {y}^(2) - 5y + 12y - 60`

`\sf \longrightarrow \: {y}^(2) + 7y - 60`

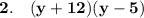
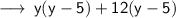
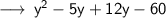
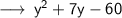
i.e, Product of two binomials.

____________________________________

`\bf3. \quad \: (x + 15)(x + 15)`

`\sf \longrightarrow \: {(x + 15)}^(2)`

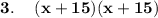
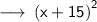
Using the algebraic identity,

`\sf {(a + b)}^(2) = {a}^(2) + {b}^(2) + 2ab`

`\sf \longrightarrow \: {x}^(2) + 225 + 30x`

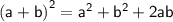
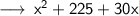
i.e, Square of a binomial.

____________________________________

`\bf \: 4. \quad \: {(x - 7)}^(3)`

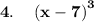
Using the algebraic identity,

`\sf \:{(a - b)}^(3) = {a}^(3) - {b}^(3) - 3ab(a - b)`

`\sf \longrightarrow \: {x}^(3) - 343 - 21 {x}^(2) + 147x`

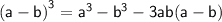
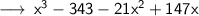
i.e, Cube of a binomial.

____________________________________

`\bf \: 5. \quad \: {(6u + 7v + 8w)}^(2)`

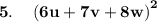
Using the algebraic identity,

`\sf{(a + b + c)}^(2) = {a}^(2) + {b}^(2) + {c}^(2) + 2ab + 2bc + 2ca`

`\sf \longrightarrow \: 36 {u}^(2) + 49 {v}^(2) + 64 {w}^(2) + 84uv + 112vw + 96wu`

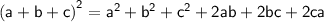
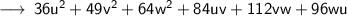
i.e, Square of a trinomial.

`\rule{200pt}{2pt}`