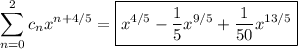By letting
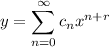
we get derivatives
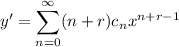

a) Substitute these into the differential equation. After a lot of simplification, the equation reduces to
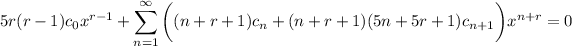
Examine the lowest degree term
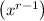 , which gives rise to the indicial equation,
, which gives rise to the indicial equation,

with roots at r = 0 and r = 4/5.
b) The recurrence for the coefficients
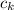 is
is
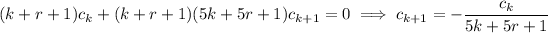
so that with r = 4/5, the coefficients are governed by

c) Starting with
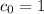 , we find
, we find
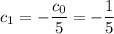
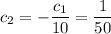
so that the first three terms of the solution are