Question

A coil of N=15 turns and radius R=10cm surrounds a long solenoid of radius r=2cm and n=103 turns/m (fig.). The current in solenoid changes as I(t)=5sin(120)t , where I is in amperes and t is in seconds. Find the induced emf in the 15-turn coil as a function of time. You must not warry about who has produced the current in the solenoid with n=103 turns/m

Answer 1

Hi there!

Recall the equation for the magnetic field produced by a solenoid:

`B = \mu_0 ni`

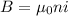
B = Magnetic field (T)
n = number of turns per unit length (103 turns/m)

i = Current in solenoid (In this instance, changes with respect to time)

Using Faraday's Law:

`\epsilon = -N(d\Phi_B)/(dt)`

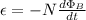
ε = Induced emf (V)
N = Number of loops in coil (15 turns)

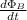`(d\Phi_B)/(dt)` = Change in magnetic flux with respect to time (Wb/s)

We know that magnetic flux is equal to:

`\Phi_B = \oint B \cdot dA = B\cdot A`

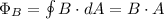
Since the cross-sectional area remains constant, we can take it out of the time-derivative. Since the current in the solenoid varies with time, we know that its magnetic field must also vary.

`(d\Phi_B)/(dt) = A * (dB)/(dt)`

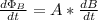
Solving for dB/dt, since the solenoid's current is the only thing changing with respect to time:

`(dB)/(dt) = \mu_0 n * (di)/(dt)`

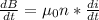
We must first differentiate I(t) using trig and chain derivative rules.

If:

`f(x) = \alpha sin(\beta t)\\\\f'(x) = (\alpha * \beta) cos(\beta t)`

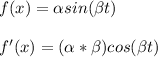
Therefore:

`(di)/(dt) = (5 * 120)cos(120t)\\\\(di)/(dt) = 600cos(120t)`

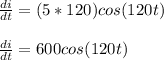
So, dB/dt equals:

`(dB)/(dt) = \mu_0 n(di)/(dt)\\\\(dB)/(dt) = (4\pi * 10^(-7))(103)(600cos(120t))\\\\(dB)/(dt) = 0.0777cos(120t)`

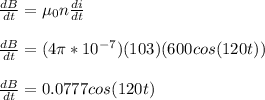
Now, substituting this expression into the equation for Faraday's Law:

`\epsilon = -N_(coil) * A * (dB)/(dt) \\\\\epsilon = -15 * \pi(0.02^2) * 0.0777cos(120t)\\\\\epsilon = \boxed{-0.001464cos(120t) \text { V}}`

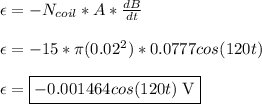
**For 'A', I used the cross-sectional area of the solenoid because there is no magnetic field produced by the solenoid in the exterior of its opening. Thus, the magnetic field remains confined to an area of A = π(0.02²) = 0.00126 m², which is the value used to calculate the magnetic flux rather than the cross-sectional area of the coil.

**Also, the (-) sign in front of the function of the induced emf simply shows how the induced E-field and consequentially emf opposes the change in the solenoid's current.