Answer:
Packing in a rectangular prism box
As the cans are cylindrical in shape, they are not able to be packed into a conventional rectangular prism box without wasted space. Therefore, we need to model the cans as rectangular prisms with the following dimensions:
- height = 4.5 cm
- width = diameter = 2 × radius = 2 × 1.7 cm = 3.4 cm
- length = width = 3.4 cm
Volume of a rectangular prism = width × length × height
= 3.4 × 3.4 × 4.5
= 52.02 cm³
Therefore, the volume of space a can will take up in the box is 52.02 cm³ (regardless of the orientation in which they are packed).
To calculate how many cans can be stored in a box with a volume of 1000 cm³, divide the volume of the box by the found volume of the space needed for one can.
Number of cans = volume of box ÷ volume of space needed for one can
= 1000 cm³ ÷ 52.02 cm³
= 19.22337562...
= 19
Therefore, the box can theoretically store a maximum of 19 cans.
Packing in a cylindrical box (tube)
If the box was a tube (cylinder) where each can could be stacked on top of each other, we can model the can as a cylinder:
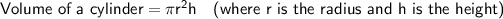
⇒ Volume of a can = π (1.7)² (4.5)
= 40.85641246... cm³
Number of cans = volume of box ÷ volume of space needed for one can
= 1000 cm³ ÷ 40.85641246... cm³
= 24.47596203...
= 24
Therefore, a cylindrical tube box can store a maximum of 24 cans.