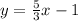Answer:
The equation of the line will be:
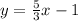
Explanation:
Given the points
Finding the slope between (3, 4) and (12, 9)
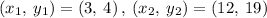
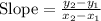
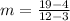
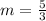
The equation of the line can be obtained using the point-slope form of the equation of the line
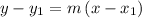
substituting the values m = 5/9 and the point (3, 4)
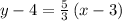
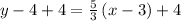
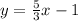
Therefore, the equation of the line will be: