Answer:
Given function:
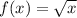
Replace f(x) for y:
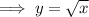
Square both sides:
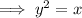
This is a sideways parabola that opens to the right, with an axis of symmetry at y = 0. (Refer to attachment 1)
If we square root this again, we get:
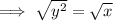
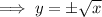
So
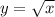 is the part of the parabola in quadrant I → (x, y)
is the part of the parabola in quadrant I → (x, y)
And
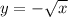 is the part of the parabola in quadrant IV → (x, -y)
is the part of the parabola in quadrant IV → (x, -y)
(Refer to attachment 2)
Therefore, the graph of the given function is attachment 3.