Question

The glide slope is the path a plane uses while it is landing on a runaway. The glide slope usually makes a 3 degree angle with the ground. A plane is on the glide slope and is 1 mile (5280) from touchdown. Find EF the planes attitude, to the nearest foot. Show your work.

Answer 1

277 feet

Explanation:

From the information given;

The slope of the glide is said to make an angle of 3° to the ground surface;

i.e.

θ = 3°

Also, there is a plane on this glide slope whose distance is 1 mile(5280 feet) away from the touchdown.

Suppose the above expression forms and angle DEF;

where;

the distance of the plane on the glide slope to the touchdown is DF

and the height in terms of altitude is EF;

Then;

Using the tangent of the trigonometric function;

`tan \theta = (EF)/(DF)`

`tan \ 3 = (EF)/(5280)`

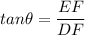
EF = 5280 × tan (3°)

EF = 5280 × 0.05240777928

EF = 276.713 feet

EF ≅ 277 feet