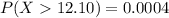Question

A machine that fills bottles on an assembly line does so according to a normal distribution, where the mean amount of liquid poured into each bottle is 11.95 ounces with a standard deviation of 0.045 ounces. If more than 12.10 ounces is poured into a bottle, it will overflow and waste the liquid.

Required:
What is the probability that a bottle has more than 12.10 ounces poured into it, causing it to overflow?

Answer 1

The probability is
`P( X > 12.10 ) =0.0004`

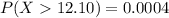
Explanation:

From the question we are told that

The mean is
`\mu = 11.95 \ ounce`

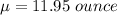
The standard deviation is
`\sigma = 0.045 \ ounce`

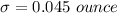
Generally the probability that a bottle has more than 12.10 ounces poured into it, causing it to overflow is mathematically represented as

`P( X > 12.10 ) = P( (X - \mu )/(\sigma ) > ( 12.10 - 11.95)/(0.045) )`

`(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )`

`P( X > 12.10 ) = P( Z > 3.33 )`

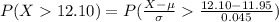
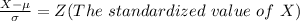
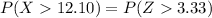
From the z table the area under the normal curve to the right corresponding to 3.33 is

`P( Z > 3.33 ) = 0.0004`

=>
`P( X > 12.10 ) =0.0004`