Question

A tower is 234 meters tall. Jaylon is looking up at the top of the tower and thinking it would be cool to string a zip line from the top of the tower to a platform that is 1.9 meters high. If the angle formed between the zip line and tower would be 76 degrees how many meters of the line is neded?

Answer 1

A length of 959.401 meters is needed for the zip line is needed to string it from the top of the tower to the platform.

Explanation:

The geometrical representation of the statement is summarized in the figure below attached. The length of the line is represented by hypotenuse of the right triangle, whose value is calculated by the help of trigonometrical relations:

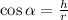`\cos \alpha = (h)/(r)` (1)

Where:

`\alpha` - Angle formed between the zip line and the tower, measured in sexagesimal degrees.

`h` - Vertical distance between the tower and the platform, measured in meters.

`r` - Length of the zip line, measured in meters.

If we know that
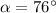`\alpha = 76^(\circ)` and
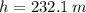`h = 232.1\,m`, then the length of the zip line is:

`r = (h)/(\cos \alpha)`

`r = (232.1\,m)/(\cos 76^(\circ))`

`r = 959.401\,m`

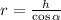
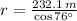
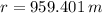
A length of 959.401 meters is needed for the zip line is needed to string it from the top of the tower to the platform.