Answer:
a) 0≠ -10
b) x= -3
c)y= 0
Explanation:
a) 3-4x=-7-4x
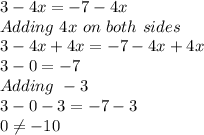
So, this equation has no solution as both sides are not equal.
b)

Solving:
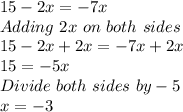
So, this equation has one solution
c) 7(y-3)=6y-21
Solving:
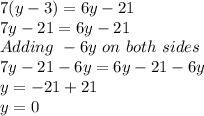
So, this equation has one solution.
1. Write equation with no solution. 3-4x=-7-4x (check solution of a)
2. Write equation with one solution. 7(y-3)=6y-21 (check solution of c)
3. Write equation with infinite solution. 2x + 3 = x + x + 3
solving:
2x+3=2x+3
2x-2x+3=3
3=3
When both sides are equal, the equation has infinite solutions.