Answer:
The given statement that value 5 is an upper bound for the zeros of the function f(x) = x⁴ + x³ - 11x² - 9x + 18 will be true.
Explanation:
Given

We know the rational zeros theorem such as:
if
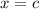 is a zero of the function
is a zero of the function
 ,
,
then
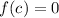 .
.
As the
 is a polynomial of degree
is a polynomial of degree
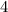 , hence it can not have more than
, hence it can not have more than
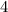 real zeros.
real zeros.
Let us put certain values in the function,
 ,
,
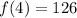 ,
,
 ,
,
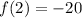 ,
,
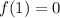 ,
,
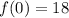 ,
,
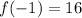 ,
,
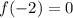 ,
,
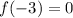
From the above calculation results, we determined that
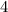 zeros as
zeros as
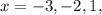 and
and
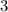 .
.
Hence, we can check that

Observe that,
 ,
,
 increases rapidly, so there will be no zeros for
increases rapidly, so there will be no zeros for
 .
.
Therefore, the given statement that value 5 is an upper bound for the zeros of the function f(x) = x⁴ + x³ - 11x² - 9x + 18 will be true.