Question

which triangle congruence criteria can always be used to prove two triangles congruent in a coordinate plane?

Answer 1

The Side-Side-Side congruency criteria

Explanation:

The Side-Side-Side (SSS) congruency criteria can always be used to prove two triangles are congruent in a coordinate plane

When two triangles are presented in the coordinate plane, the coordinates of the vertices of both triangle will be given by the coordinates of their points on the coordinate plane

The length of the sides of each triangle will be given by the distances, d₁, d₂, d₃, between the coordinates of their vertices as follows;

`d = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

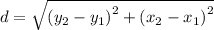
The two triangles are congruent when the length of the three sides d₁, d₂, and d₃ of one triangle ABC, are congruent to the three sides d'₁, d'₂, and d'₃ of the other triangle A'B'C'.